(Image from http://www.festungguernsey.supanet.com/about_us.htm)
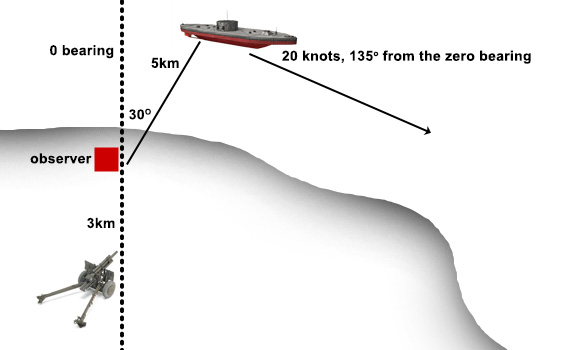
Imagine an observer with a stereoscopic rangefinder and a telephone, camouflaged on a seashore. The observer is 3km ahead of a cannon located further inland for concealment. The bearing is between the cannon and the observer is, for the purposes of communication ease, zero.
Now, for the math and geometry questions:
1. The observer sees a ship that is 5km away at bearing 30 by the rangefinder and compass. Assuming the ship is neither head-on nor in profile, how can the observer calculate speed and the direction of travel of the ship from observation? Assume no readily visible landmarks behind the ship.
2. Let’s say that the ship is at this moment 5km away at bearing 30 as observed from the forward post. What are the distance and the bearing at this moment from the battery which is 3km behind the observer?
3. Let’s say that the ship’s direction of travel is 135 degrees from the zero reference bearing (going over the observer’s right shoulder) and the speed is 20 knots (approx. 36km/h). If it took the cannon crew fifty seconds to calculate the firing solution, and the shell flight time is ten seconds, at which point relative to the cannon (distance and bearing) should the gun be aimed?
4. Assuming the ship is 100m long and the combined side and deck projection at the 30 degree angle of the shell impact is 25m, what is the probability of a first-round hit from the cannon with 1 minute of angle dispersion?
Having performed these calculations, meditate on the addition of gun platform movement to simulate ship to ship combat. Increase range to 10km. Increase dispersion over time as the barrels heat up. I am beginning to understand why ballistic computers and firing synchronizes (for shooting all guns at a consistent point in time during the wave roll) were such a big deal. And why trained specialist meant victory in artillery exchanges on land and sea. Upgrade the difficulty once more for air to air combat, and we see why gun turrets went away despite remotely operated guns with individual mechanical fire computers.
Maybe this is more like 7th grade, which would not have been beyond the 1930s students who spent more time on the basics.

You’re bringing back memories of hours upon hours upon hours spent scratching away at moboards, Oleg.
Stop that.
the math is not complicated and once you do it ALL THE TIME, it is even easier. However the math is also easy to mess up, especially under pressure.
Ship to ship with rolling seas is a whole other can of worms.
The Northrop P-61 Black Widow had a lovely radar and a gun turrent for air to air interception during WWII. It was, by some tests, faster than the more famous Mosquito.
Ah, the fire control problem! This and the related problems of armor protection and armor-piercing shells have been of considerable interest to me lately. It’s amazing to me that very bright men, notably Arthur Pollen in the UK and Hannibal Ford here in the United States, devised various devices that could solve this problem with considerable speed and accuracy long, long before the computer chip was ever thought of.
Thanks for the mention of H. Ford. I found this paper about him. Very interesting.
http://web.mit.edu/STS.035/www/PDFs/Newell.pdf
1). One way to view this is a coordinate conversion problem. The observer is locating the ship in polar coordinates (compass direction plus distance) relative to his location. Converting that to basic cartesian coordinates (x, y) uses just a little trigonometry. And given *two* locations plus the time between them, you can calculate course and speed. You can’t of course get the speed from a single observation.
I don’t know how well this would work in practice; but if you know from (for example) the basic class of ship you’re observing (this works better, obviously, for common warship types than it does for random commercial ships, which are less standardized) how long the ship is really, you can figure the degree of rotation of the ship from the foreshortening (you also have to account for the distance, but the rangefinder gives you that directly). (Well, you can figure one of *four* directions; but if you can see the ship well enough to identify the class you can also tell what direction it’s going, so you can pick which of the four directions it’s actually going in). This is mathematically valid, but depends *both* on the accuracy of the distance measurement *and* on the accuracy of the observed length measurement, so the error might be too big to be very useful in practice. However, it gets you an answer on the course more quickly, you don’t have to wait for it to travel far enough for a second position to show what the actual course is.
(I can work through the math for these I think, but it would be *work*; I trained as a pure mathematician 40 years ago but have been spending my actual life as a computer programmer. And this is *applied* math anyway. So I might consider doing the actual work if it’s important to you, but not just for fun.)
4) What assumption are you making about the distribution of hits within the 1 MOA dispersion? Flat, or normal distribution (the second is I believe closer to right)?
Back during the Napoleonic wars, when mostly it was smoothbore cannon, they were already getting serious about the math (though not so much for shipboard use; too many variables there). And not too long after *that* they had to start taking variation in air density with altitude into account for longer (hence higher) trajectories. And these were among the kinds of tables that early mechanical computers were built to calculate (people started trying in the 1820s, first working “difference engine” was in the early 1840s).
Normal distribution is closer to reality, but we can substitute flat because we are also simplifying the target shape relative to the more complex reality.
In practice; Each battery was given a certain number of dye marker shells. The gun plotter (observer) would guesstemate the range, bearing, relative speed. All batteries would fire AHEAD of the ship. The observer would call corrections based on fall of shot. A typical order for coastal guns might be: “Battery yellow ;(the color of the dye marker shell) Straddle. right 5 mil. fire for effect”. You must remember that until the advent of the analog ballistic computer in the 1930’s, it was common for a gun battery to fire hundreds of shots at a ship without a single hit .
I know the answers boil down to “trigonometry”, but I promptly forgot it after high school.
(In the real world everyone used trig tables anyway.)
Redleg this is Telescope, Adjust fire polar.
Observer grid AB123456, target 0530 magnetic, range 5km
one ship in the open, HE in adjust, ICM in effect over.
DPICM covers for laziness.
This is precisely why the FDC uses the AFATDS instead of “charts ‘n’ darts” and the FO brackets his target. This is also why I wasn’t FDC or an FO.
Exactly.
A reorganization in my National Guard division required that I, an Infantry officer, attend the Field Artillery Officer Advanced Course to be qualified for my reassignment. Tactics, logistics, and operations were the same but gunnery made me wish I’d paid better attention in trig class.
Got through it and got promoted, but I stayed away from the FDC. Didn’t want to kill the wrong people.